Quick Sort
- Runtime: 0 (n Log (n)) Average, 0 (n*2) Worst Case. Memory: 0 (log (n) ) .
- In quick sort, we pick a random element and partition the array, such that all numbers that are less than the partitioning element come before all elements that are greater than it.
- The partitioning can be performed efficiently through a series of swaps.
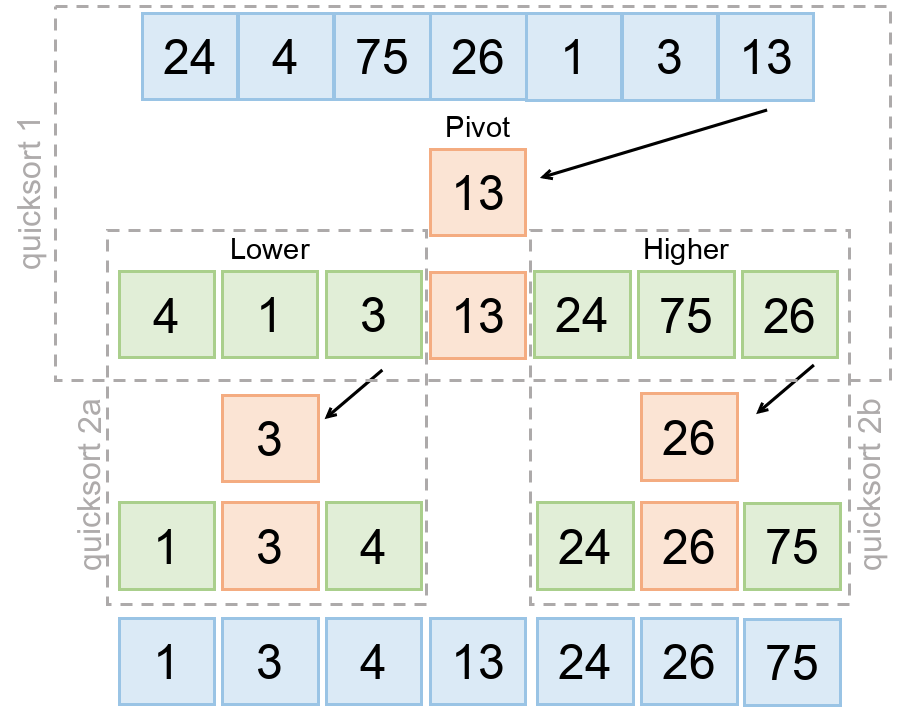
- If we repeatedly partition the array (and its sub-arrays) around an element, the array will eventually become sorted.
- However, as the partitioned element is not guaranteed to be the median (or anywhere near the median), our sorting could be very slow. This is the reason for the 0 (n**2) worst case runtime.
def quickSort(Array):
return divide(Array)
def divide(Array):
if len(Array) <= 1:
return Array
else:
pivote = Array[0]
left = divide([elt for elt in Array if elt < pivote])
right = divide([elt for elt in Array if elt > pivote])
array = concure(Array, left, pivote, right)
return array
def concure(Array, left, pivote, right):
return left + [pivote] + right
print(quickSort([6,5,4,3,2,1]))