Topological Sort Kahns Algorithm
- Video source
- Has the same properties as Topological sort DFS Version
- Also known as
Topological sort BFS
- Also known as
- The intuition behind kahn's algorithm
- Repeatedly remove nodes without any dependencies from the graph and add them to the topological ordering
- As nodes without dependencies(and their outgoing edges) are removed from the graph, new nodes without dependencies are created/born
- We repeat removing nodes without dependencies from the graph until all nodes are processed, or a cycle is detected
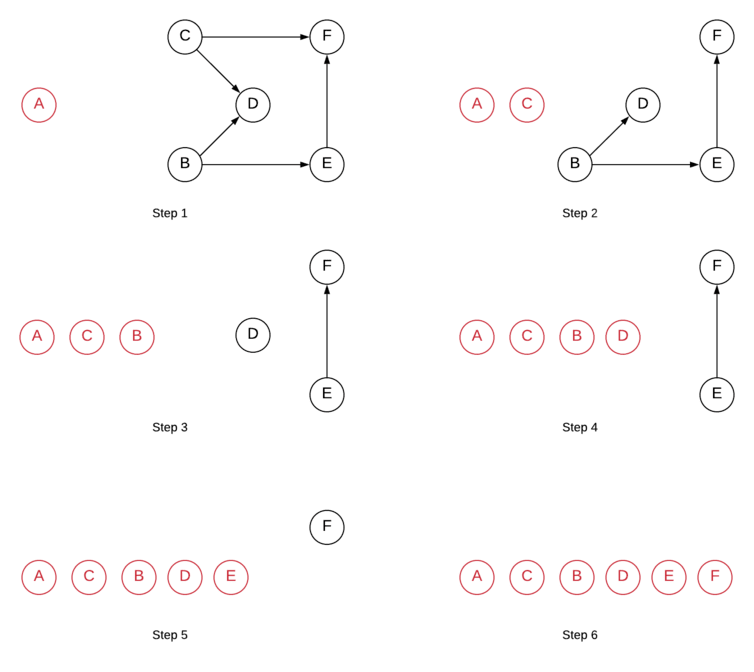
Algorithm Explanation
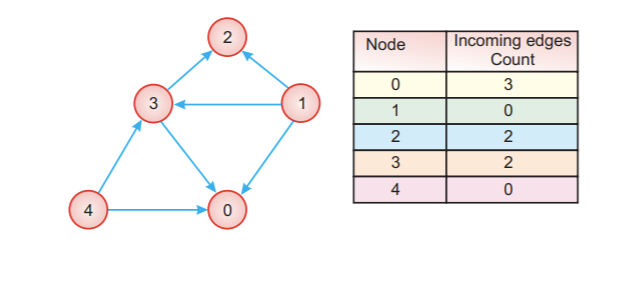
The first node in the topological ordering will be the node that doesn't have any incoming edges. Essentially, any node that has an in-degree of 0 can start the topologically sorted order. If there are multiple such nodes, their relative order doesn't matter and they can appear in any order.
- Initialize a queue,
Qto keep a track of all the nodes in the graph with 0 in-degree. - Iterate over all the edges in the input and create an adjacency list and also a map of node v/s in-degree.
- Add all the nodes with 0 in-degree to
Q. - The following steps are to be done until the
Qbecomes empty.- Pop a node from the
Q. Let's call this node,N. - For all the neighbors of this node,
N, reduce their in-degree by 1. If any of the nodes' in-degree reaches 0, add it to theQ. - Add the node
Nto the list maintaining topologically sorted order. - Continue from step 4.1.
- Pop a node from the
q = deque()
in_degree = defaultdict(int) #notice -> we count the incoming edges to a node
for node in graph:
for edge in node:
in_degree[edge] += 1
for node in graph:
if in_degree[node] == 0:
q.append(node)
order = []
while q:
node = q.popleft()
order.append(node)
for edge in node:
in_degree[edge] -= 1
if in_degree[edge] == 0:
q.append(edge)
if len(order) != number_of_nodes:
return null #graph contains cycle
return order